べん毛モーターの回転計測において，慣性力，遠心力は考慮すべきか？

遠心力の影響の検討

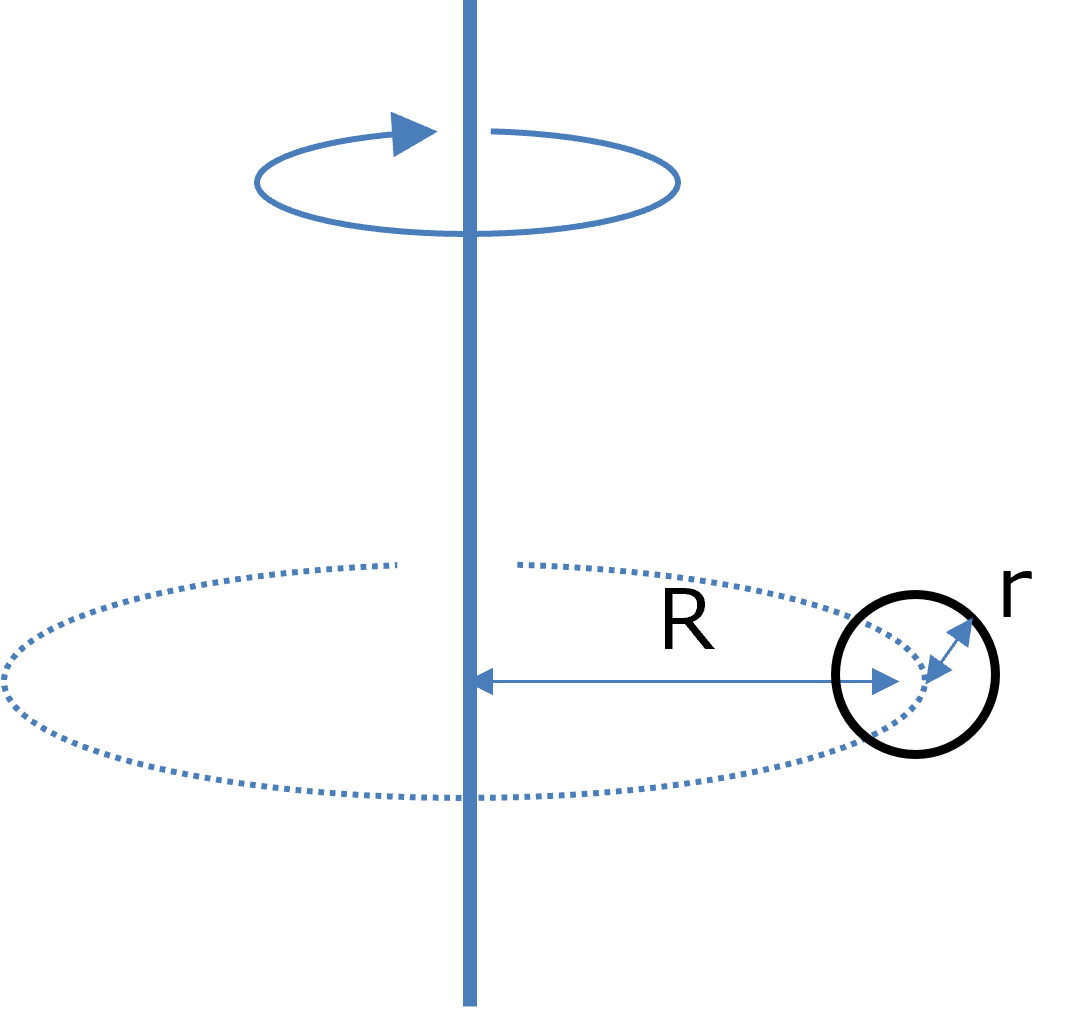
半径Rの円周上を半径ｒのビーズが回転する系を考えます．

遠心力の影響を，回転する際の並進の粘性抵抗と比較していきます．

遠心力：\( \Large \displaystyle F_{centrifugal forces}=m' \ R \ \omega^2 \)

粘性抵抗：\( \Large \displaystyle F_{viscosity}= 6 \pi \eta r \cdot v \)

となります．ここでｍ‘は浮力を考慮した実効質量です．

慣性力の場合には浮力を考慮する必要はありませんが，遠心力の場合には，溶媒の密度との関係が重要となります．

例に挙げると，
　重力という力が働いているときに，木片は落下する（木片の密度＞空気の密度）
　　　しかし，
　水中の木片は上昇する（木片の密度＜水の密度）
となります．遠心機において，溶媒（水）より軽い油分などは遠心チューブの上面にたまることからも理解できます．

遠心力は，

実行質量，m'，は同じ体積の溶媒の質量を引いた値なので，

\( \Large \displaystyle m' = V ( \rho_{sample} - \rho_{water}) \)

\( \Large \displaystyle = \frac{4}{3} \pi r^3 ( 1.05 \times 10^3 - 1.00 \times 10^3) \)

\( \Large \displaystyle = \frac{4}{3} \pi r^3 \cdot 50 \)

水溶液中のポリスチレンビーズの運動を考えるので，

\( \Large \displaystyle r = 0.5 \ \mu m = 5 \times 10^{-7} \ [m] \)

を代入して，

\( \Large \displaystyle m' = \frac{4}{3} \pi \left( 5 \times 10^{-7} \right)^3 \cdot 50 = 2.6 \times 10^{-17} [kg]\)

遠心力は，回転速度が，100 Hz，の場合，回転中の回転半径Rを大きめに，

\( \Large \displaystyle R = 0.5 \ \mu m = 5 \times 10^{-7} \ [m] \)

として，

\( \Large \displaystyle F_{centrifugal forces}=m' \ R \ \omega^2 = 2.6 \times 10^{-17} \cdot 5 \times 10^{-7} \cdot (200 \pi)^2 = \pi^2 \cdot 5.2 \times 10^{-19} = 5.17 \times 10^{-18} [N] \)

となります．

一方，粘性抵抗は，

円周上の回転速度は，

\( \Large \displaystyle v=\frac{2 \pi R}{ 1/100} = 2 \pi \cdot 5 \times 10^{-7} \cdot \pi \cdot 5 \times 10^{-7} = \pi \cdot 10^{-5} = 3.14 \times 10^{-5} [m/s] \)

となるので，

\( \Large \displaystyle F_{viscosity}= 6 \pi \eta r \cdot v = 6 \pi \cdot 10^{-3} \cdot 5 \times 10^{-7} \cdot 3.14 \times 10^{-5} = \pi^3 \cdot 3 \times 10^{-14} = 2.96 \times 10^{-13} [N] \)

まとめると，

遠心力：\( \Large \displaystyle F_{centrifugal forces} \hspace{10pt} = \ 5.17 \times 10^{-18} [N] \)

粘性抵抗：\( \Large \displaystyle F_{viscosity} \hspace{40pt} = \ 2.96 \times 10^{-13} [N] \)

となり，約5桁遠心力のほうが小さいことがわかります．

したがって，ミクロな世界での水溶液の回転運動においては，遠心力は無視してかまわない，ことになります
（非常に高速であったりした場合は適用できませんが．．．）

次ページには，慣性モーメント，で検討していきます．